Welcome to my CPP project, which focuses on implementing various image processing algorithms from scratch such as filtering, edge detection, corner detection, SIFT detector, relevant mathematical functions and more. In addition I implemented my own matrix class that include many arithmetic and mathematical functions as well as suitable operators.
- At this section I will introduce the MyMatrix and Image classes, apart of them there are other mathematical and helpful functions in the Funcs.h file, such as Convolution, Local Max, Gaussian Set initializer and more.
At this project I implemented every algorithm from scratch, In order to do that I built the “MyMatrix” class. By providing a flexible and efficient matrix data structure, the class simplifies the process of implementing complex algorithms that require matrix operations. Here is a summary of the methods provided by the MyMatrix class:
| Property | Description |
|---|---|
double** _matrix |
A pointer to a 2D array of double values that represents the matrix data. |
int _n |
An integer that represents the number of rows in the matrix. |
int _m |
An integer that represents the number of columns in the matrix. |
| Method | Description |
|---|---|
MyMatrix() |
Default constructor. Initializes zeros values 3x3 matrix. |
MyMatrix(int n, int m) |
Constructs a zero values matrix of size n x m. |
MyMatrix(const MyMatrix& other) |
Copy constructor. Creates a new matrix that is a copy of other. |
MyMatrix(const Mat& other) |
Creates a new matrix that is a copy of the given cv::Mat object. |
~MyMatrix() |
Destructor. Deletes dynamically allocated memory. |
void setMatrix(int n = 3, int m = 3) |
Sets zero values matrix of size n x m . Default is 3x3. |
int getRows() const |
Returns the number of rows in the matrix. |
int getCols() const |
Returns the number of columns in the matrix. |
double max() const |
Returns the maximum value in the matrix. |
double min() const |
Returns the minimum value in the matrix. |
MyMatrix mul(const MyMatrix& other) const |
Returns the matrix product of this and other. |
MyMatrix T() const |
Returns the transpose of the matrix. |
MyMatrix abs() const |
Returns a new matrix with the absolute values of each element. |
MyMatrix integ() const |
Returns a new matrix where each element is the cumulative sum of the elements above and to the left of it. |
MyMatrix localMax(int window_Size = 3) const |
Returns a new matrix with local maxima in every window by the window size. |
void clean_localMax(MyMatrix& res,double max, int window_Size,int indexX, int indexY, int rows, int cols) const |
Private helper function to clean local maxima. |
void sort() |
Sorts every row of the matrix in ascending order by Merge Sort Algorithm. |
void cvNorm() |
Normalizes the matrix so that its sum of squares is equal to 1. |
Mat getCV_mat() |
Returns the matrix as a cv::Mat object. |
void minMax(double factor=100); |
Min Max Normalization |
operator=(const MyMatrix& other) |
Assignment operator. Copies the matrix from other to this. |
operator==(const MyMatrix& other) const |
Equality operator. Returns true if this is equal to other. |
operator+(const MyMatrix& other) const |
Addition operator. Returns the sum of this and other. |
operator-(const MyMatrix& other) const |
Subtraction operator. Returns the difference of this and other. |
operator double() const |
Conversion operator. Returns the sum of the matrix as a double. |
operator*(const MyMatrix& other) const |
Matrix multiplication operator. Returns the matrix of the element-wise multiplication of this and other. |
operator*(double num) const |
Scalar multiplication operator. Returns the product of this and num. |
operator*(int num) const |
Scalar multiplication operator. Returns the product of this and num. |
friend ostream& operator<<(ostream& out, const MyMatrix& other) |
Overloads the << operator for getting easy output of MyMatrix objects. |
double*& operator [](const int& index) const |
Overloads the [] operator to allow easy access to elements in a MyMatrix object. |
friend istream& operator>>(istream& in, MyMatrix& other) |
Overloads the >> operator to allow inserting input values to MyMatrix objects. |
This class can be used to perform various image processing tasks or as a foundation for building more advanced image processing algorithms.
| Property | Description |
|---|---|
MyMatrix _histogram |
A MyMatrix object representing the image histogram. |
string _path |
A string representing the path to the image file. |
MyMatrix _gmat |
A MyMatrix object representing the image matrix. |
| Method | Description |
|---|---|
MyMatrix calHist()const |
Calculates and returns the histogram of the image |
Image(const string file_name) |
Constructor that reads an image from a file |
Image(int rows, int cols,string path="None") |
Constructor that creates an image with specified rows and columns |
Image(const MyMatrix& other, string path = "None") |
Constructor that creates an image from a matrix |
void setPath(string path) |
Sets the path of the image |
void set_out_Path(string path,string input) |
Adding the algorithm type for the output path |
void setGmat(int rows, int cols) |
Sets zero values matrix of the image with specified rows and columns |
void setGmat(const MyMatrix& other) |
Sets the matrix of the image from a matrix |
void setHist() |
Calculates and sets the histogram of the image |
int getRows()const |
Returns the number of rows in the image |
int getCols()const |
Returns the number of columns in the image |
MyMatrix getHist()const |
Returns the histogram of the image |
MyMatrix getGmat()const |
Returns the matrix of the image |
string getPath()const |
Returns the path of the image |
void display()const |
Displays the image |
void save()const |
Saves the image |
int getHistPercentile(const int p)const |
Returns the p-th percentile in the histogram |
void showHist()const |
Displays the histogram of the image |
void drawHist(const vector<double>& data, Mat3b& dst, int binSize = 3, int height = 0)const |
Draws the histogram of the image |
Image ContrastStretch()const |
Applies contrast stretching to the image |
Image equalize()const |
Applies histogram equalization to the image |
Image median(const int size = 3)const |
Applies median filtering to the image with specified kernel size |
Image gausBlur(const int size = 3, double const sigma = 0.477)const |
Applies Gaussian blur to the image with specified kernel size and sigma |
Image edgeDetect(const string& type,int size=3,double sigma=0.5)const |
Detects edges in the image using the specified method-SobelX/SobelY/Sobel/Laplac/Canny |
Image corners(int size, double threshold_value= 5.1 * (pow(10, 7))) |
Finds corners in the image using the specified method |
Image sift(double s=1.2, int gausSize = 15, double sigma = 1,int setSize=10, int window_Size=100) |
Applies SIFT feature extraction to the image |
Image drawCirc(MyMatrix* maxSet,int setSize,int thickness,double radius, int factor=1.2)const |
Draws circles around the detected features in the image |
This project really easy to use, in the following sections i will describe how to start use it, i will give various examples and some theory explanations.
-In oreder to use this project you just have to clone it:
$ git clone https://github.com/yuvalaza/ImageProcessingCPP.git
In addition, in this project I used OpenCV for loading, displaying and saving images. If you didn’t install OpenCV yet , you can follow this guide: OpenCV Installation Guide
At this section I will describe few algorithms that I implemented in this project.
-
2D Convolution
The 2D convolution of two discrete functions f(x,y) and g(x,y) is defined as:
$(f \ast g)[n,m] = \sum\limits_{k=-\infty}^{\infty}\sum\limits_{l=-\infty}^{\infty}f[k,l] \cdot g[n-k,m-l]$ -
Gaussian Kernel
$M_{i,j}=\frac{1}{2\pi\sigma^2}\exp(-\frac{1}{2}\frac{i^2+j^2}{\sigma^2})$
Where${\sigma^2}$ is the variance. -
Discrete Gradient
$\nabla$ Operator
Finite difference approximations:
$\frac{\partial I}{\partial x}\approx\frac{1}{2 \epsilon} \left( (I_{i+1,j+1} - I_{i,j+1}) + (I_{i+1,j} - I_{i,j}) \right)$
$\frac{\partial I}{\partial y}\approx\frac{1}{2 \epsilon} \left( (I_{i+1,j+1} - I_{i+1,j}) + (I_{i,j+1} - I_{i,j}) \right)$
This operator can be implemented as Convolution. The Gradient magnitude:
$|\nabla I| = \sqrt{(\frac{\partial I}{\partial x})^2 + (\frac{\partial I}{\partial y})^2}$
Over the last few decades , a variety of gradient operators have been proposed like: Roberts Operator, Pewitt, and the one I used in this project, Sobel. -
Discrete Laplacian
$\nabla^2$ Operator:
Finite difference approximations:
$\frac{\partial^2 I}{\partial x^2}\approx\frac{1}{ \epsilon^2} ( (I_{i-1,j} -2 I_{i,j} + I_{i+1,j} )$
$\frac{\partial^2 I}{\partial y^2}\approx\frac{1}{ \epsilon^2} ( (I_{i,j-1} -2 I_{i,j} + I_{i,j+1} )$
and we get that:
$\nabla^2 I\approx\frac{\partial^2 I}{\partial x^2}+\frac{\partial^2 I}{\partial y^2}$
As well As the Gradient Operator, the Laplacian Operator can be implemented as Convolution . -
Canny Edge Detector
- Smooth Image with 2D Gaussian.
- Compute Image Gradient using Sobel Operator:
$(\nabla n_\sigma \ast I)$
- Find Gradient Magnitude at each pixel
- Find Gradient Orientation at each Pixel
- Compute Laplacian along the Gradient Direction at each pixel
- Find Zero Crossings in Laplacian to find the edge location
- Smooth Image with 2D Gaussian.
-
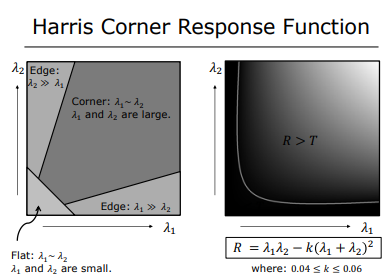
Harris Corner Detection
This algorithms is based on fitting ellipse to the pixel’s intensity distribution.
Lets define${\lambda{_1}}$ as the length of the semi-major axis of the ellipse which is also equal to maximum second moment E_max,
and${\lambda{_2}}$ as the length of the semi-minor axis which is also equal to minimum second moment E_min.
In addition, lest define the Second Moments for a Region:
$a={\Sigma}{(I_x[i])^2}$ ,$b=2{\Sigma}{(I_x[i]}{I_y[i])}$ ,$c={\Sigma}{(I_y[i])^2}$ where:
${\lambda_{1}}=\frac{1}{2}(a+c+\sqrt{b^2+(a-c)^2})$
${\lambda_{2}}=\frac{1}{2}(a+c+\sqrt{b^2-(a-c)^2})$ Harris has designed a simple expression, called the response function, that maps
${\lambda_{1}}$ and${\lambda_{2}}$ to a single number R which help us to decide if we found a corner:
-
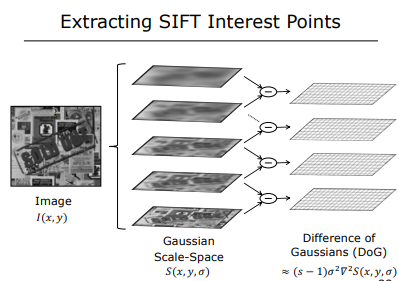
SIFT Detector
- Given an image, we first create the stack
$S_{(x,y,\sigma)}$ of images by convolving the original image with Gaussians of increasing sigma
- In order apply the NLoG operator we will find the difference between all pairs of the
$S_{(x,y,\sigma)}$ .
- Finding the extrema in this stack of images.
- In order to suppress the effects of noise, we can use a threshold to filter out weak extrema.
- Given an image, we first create the stack
- On this section you will find some examples of how to use some of the algorithms and and their outputs as well.
You can find it in the Commands And Examples file
- A C++ compiler such as GCC or Clang
- A text editor or integrated development environment (IDE) such as Visual Studio Code or Code::Blocks
Fundamentals of Image Processing- By Ian T. Young ,Jan J. Gerbrands, Lucas J. van Vliet.
Features and Boundaries Course- By Columbia University
https://stackoverflow.com/
MIT License
Copyright (c) [2023] [Yuval Azachi]
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.