TempLogic is a library of temporal logics that admit quantitative semantics. It currently supports Signal Temporal Logic (STL), Tree Spatial Superposition Logic (TSSL) and Spatial-Temporal Logic (SpaTeL) to varying degrees:
- All three support the construction of every syntactically valid formula and computation of quantitative semantics.
- STL has a parser, inference and MILP encoding.
- TSSL has inference.
- SpaTeL inference is a work in progress.
You need Python3.8 or newer and the use of virtualenv's or similar is encouraged. The inference modules require Weka 3 installed. The MILP encoding module requires Gurobi 7 or newer.
Clone the repository with:
$ git clone https://github.com/franpenedo/templogic.git
Install with PIP:
$ pip install templogic
If you want to use the inference modules, make sure you have Weka 3 installed, then run:
$ pip install templogic[inference]
If you want to use the MILP encoding module, make sure you have Gurobi and its Python package (gurobipy) installed, then run:
$ pip install templogic[milp]
Temporal logics are formal languages capable of expressing properties of system (time-varying) trajectories. Besides the usual boolean operators, temporal logics introduce temporal operators that capture notions of safety ("the system should always operate outside the danger zone"), reachability ("the system is eventually able to enter a desired state"), liveness ("the system always eventually reaches desired states"), and others. Once a property is expressed, automatic tools based on automata theory, optimization or probability theory are able to check wether a system satisfies the property, or synthesize a controller such that the system is guaranteed to satisfy the specification.
For some scenarios, a binary measure of satisfaction is not enough. For example, one might want to operate a system such that safety is not only guaranteed but robustly guaranteed. In other applications, a not satisfying best effort might provide an engineer with clues about mistakes in the specification or guide more expensive algorithms towards satisfaction. For these situations, some temporal logics can be equiped with quantitative semantics, i.e., a real score r such that a trajectory satisfies a specification if and only if r > 0. If one considers a temporal logic formula as the subset of trajectories that satisfy it, the score r can be interpreted as the distance of a trajectory to the boundary of this set.
Consider for example Signal Temporal Logic (STL), a temporal logic based on Lineal Temporal Logic (LTL) that defines temporal bounds for its temporal operators and uses inequalities over functions of the system state as predicates. For example in STL one can express the property "always between 0 and 100 seconds the x component of the system state cannot exceed the value 50, and eventually between 0 and 50 seconds the x component of the system must reach a value between 5 and 10 and stay within those bounds at all times for 10 seconds", which would be written as the formula:
f = G_[0, 100] x < 50 ^ F_[0, 50] (G_[0, 10] (¬ (x < 5) ^ x < 10))
You can define f using Templogic as follows:
from templogic.stlmilp import stl
# `labels` tells the model how each state component at time `t` is represented
# It can also be a function of t that returns the list of variables at time `t`
labels = [lambda t: t]
# Predicates are defined as signal > 0
signal1 = stl.Signal(labels, lambda x: 50 - x[0])
signal2 = stl.Signal(labels, lambda x: 5 - x[0])
signal3 = stl.Signal(labels, lambda x: 10 - x[0])
f = stl.STLAnd(
stl.STLAlways(bounds=(0, 100), arg=stl.STLPred(signal1))
stl.STLEventually(
bounds=(0, 50),
arg=stl.STLAlways(
bounds=(0, 10),
arg=stl.STLAnd(
args=[
stl.STLNot(stl.STLPred(signal2)),
stl.STLPred(signal3)
]))))The score or robustness of a trajectory x(t) with respect to the specification f can be defined as follows:
r(x(t), f) = min {min_{t in [0, 100]} 50 - x(t),
max_{t in [0, 50]} (min_{t in [0, 10]} (min {-(5 - x(t)), 10 - x(t)})) }
In Templogic, you must define a model that understands how to translate state variables
at time t used in signals:
class Model(stl.STLModel):
def __init__(self, s) -> None:
self.s = s
# Time interval for the time discretization of the model
self.tinter = 1
def getVarByName(self, j):
# Here `j` is an object that identifies a state variable at time `t`
# in the model, generated by the functions in `labels` above.
# In our case it is simply the index in the array that contains the
# trajectory
return self.s[j]You can then compute the score for a particular model:
s = [0, 1, 2, 4, 8, 4, 2, 1, 0, 1, 2, 6, 2, 1, 5, 7, 8, 1]
model = Model(s)
score = stl.robustness(f, model)An obvious framework to work with temporal logics with quantitative semantics would be to reformulate verification and synthesis problems as optimization problems, where the objective is to maximize the score r. However, as can be seen above, the definition of the score is non-convex and discontinuous, which makes it particularly difficult to include directly either as an objective function or as a constraint in efficient optimization algorithms, such as those used in Linear Programming. Instead, an equivalent reformulation can be used to transform the score definition into a series of mixed-integer linear constraints. The solution of Mixed-Integer Linear Programs (MILPs) is in general very expensive (double exponential), but very good heuristic techniques can be used to efficiently solve interesting problems in practice. As an example, consider the following MILP reformulation of the function min {x, y}:
r <= x
r <= y
r > x - M d
r > y - M d
d in {0, 1}
where M is a sufficiently big number chosen a priori. The auxiliary variable r can
now be used as optimization objective or as a constraint (for example r > 0 for satisfaction).
As seen above, robustness in STL are defined as nested max and min operations and
can be fully encoded in this fashion. In Templogic, we define encodings for the popular
MILP solver Gurobi. You can create an MILP model and add
the robustness of the STL formula f defined above as follows:
from templogic.stlmilp import stl_milp_encode as milp
m = milp.create_milp("test")
# Define here your model. Make sure you label each variable representing
# a system variable at time `t` consistently with the `labels` parameter
# to the STL Signals. For example labels may be defined as:
# labels = [lambda t: f"X_0_{t}"]
# which would, for t=5, fetch the variable `X_0_5` from the Gurobi model
m.addVar(...)
m.addConstr(...)
# `r` contains a Gurobi variable with the robustness of f.
r, _ = milp.add_stl_constr(m, "robustness", f)
# You can use this variable in constraints
m.addConstr(r > 0)
# or set a weight in the objective function for it
r.setAttr("obj", weight)You can find more helper functions in the stl_milp_encode module.
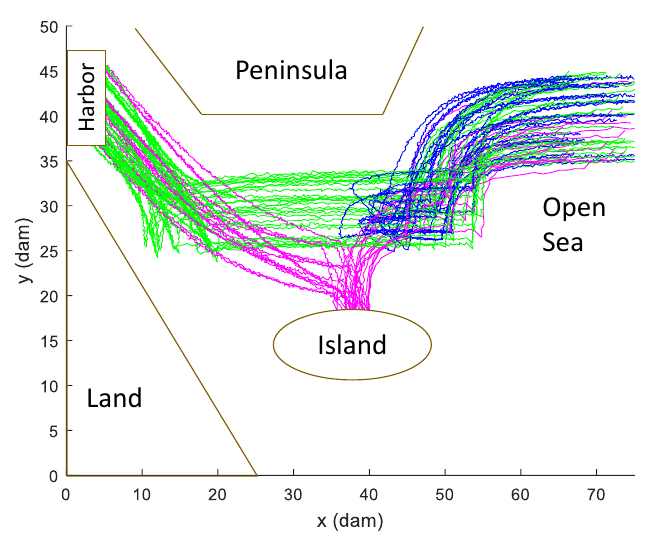
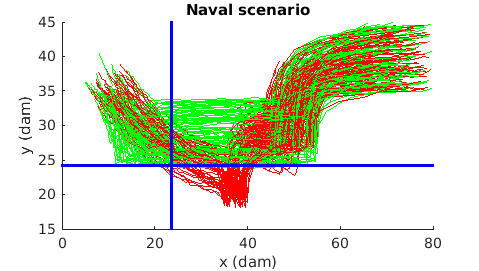
STL inference is the problem of constructing an STL formula that represents "valid" or "interesting" behavior from samples of "valid" and "invalid" behavior. For example, suppose you have a set of trajectories of boats approaching a harbor. A subset of trajectories corresponding with normal behavior are labeled as "valid", while the others, corresponding with behavior consistent with smuggling or terrorist activity, are labeled "invalid". You can encode this data in a Matlab file with three matrices:
- A
datamatrix with the trajectories (with shape: number of trajectories x dimensions x number of samples), - a
tcolumn vector representing the sampling times, and - a
labelscolumn vector with the labels (in minus-one-plus-one encoding).
You can find the .mat file for this example in
templogic/stlmilp/inference/data/Naval/naval_preproc_data_online.mat. In order to
obtain an STL formula that represents "valid" behavior, you can run the command:
$ lltinf learn templogic/stlmilp/inference/data/Naval/naval_preproc_data_online.mat
Classifier:
(((F_[74.35, 200.76] G_[0.00, 19.84] (x_1 > 33.60)) & (((G_[237.43, 245.13] ...A full description of the decision tree approach to STL inference can be found in our peer-reviewed publication Bombara, Giuseppe, Cristian-Ioan Vasile, Francisco Penedo, Hirotoshi Yasuoka, and Calin Belta. “A Decision Tree Approach to Data Classification Using Signal Temporal Logic.” In Proceedings of the 19th International Conference on Hybrid Systems: Computation and Control, 1–10. HSCC ’16. New York, NY, USA: ACM, 2016. https://doi.org/10.1145/2883817.2883843..
MILP encoding of STL has been featured in many peer reviewed publications, including our own work in formal methods for partial differential equations: Penedo, F., H. Park, and C. Belta. “Control Synthesis for Partial Differential Equations from Spatio-Temporal Specifications.” In 2018 IEEE Conference on Decision and Control (CDC), 4890–95, 2018. https://doi.org/10.1109/CDC.2018.8619313.
Our implementation of TSSL and TSSL inference is based on Bartocci, E., E. Aydin Gol, I. Haghighi, and C. Belta. “A Formal Methods Approach to Pattern Recognition and Synthesis in Reaction Diffusion Networks.” IEEE Transactions on Control of Network Systems PP, no. 99 (2016): 1–1. https://doi.org/10.1109/TCNS.2016.2609138.
SpaTeL was first introduced in Haghighi, Iman, Austin Jones, Zhaodan Kong, Ezio Bartocci, Radu Gros, and Calin Belta. “SpaTeL: A Novel Spatial-Temporal Logic and Its Applications to Networked Systems.” In Proceedings of the 18th International Conference on Hybrid Systems: Computation and Control, 189–198. HSCC ’15. New York, NY, USA: ACM, 2015. https://doi.org/10.1145/2728606.2728633.
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.
Copyright (C) 2016-2021, Francisco Penedo Alvarez ([email protected])