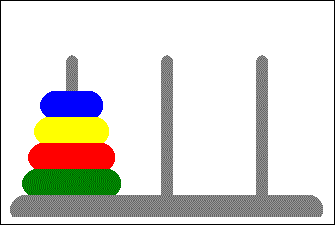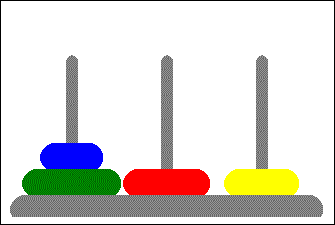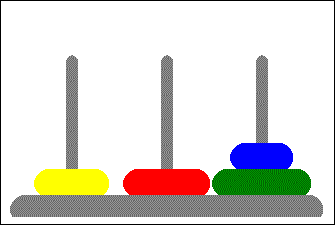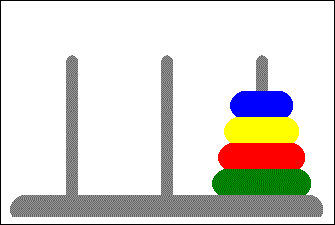
A classic CS (and interview) problem where you are asked to move rings of various sizes from the left tower through a middle tower to the rightmost one. The only constraints are you must move only one ring at a time and a ring cannot be moved on top of a smaller ring.
The instructions for the case where rings = 3 follows:
| step | left tower | middle tower | right tower |
|---|---|---|---|
| 1. Start | 123 | ||
| 2. L -> R | 23 | 1 | |
| 3. L -> M | 3 | 2 | 1 |
| 4. R -> M | 3 | 12 | |
| 5. L -> R | 12 | 3 | |
| 6. M -> L | 1 | 2 | 3 |
| 7. M -> R | 1 | 23 | |
| 8. L -> R | 123 |
Your task is to generalize this algorithm for the case where rings = n, a positive integer. Assume 3 towers.