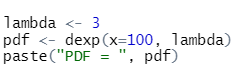a) Peluang Distribusi Geometrik dapat diperoleh dengan menggunakan fungsi dgeom(x, p), di mana x = 3 dan p = 0.2
Diperoleh hasil sebesar 0.1024
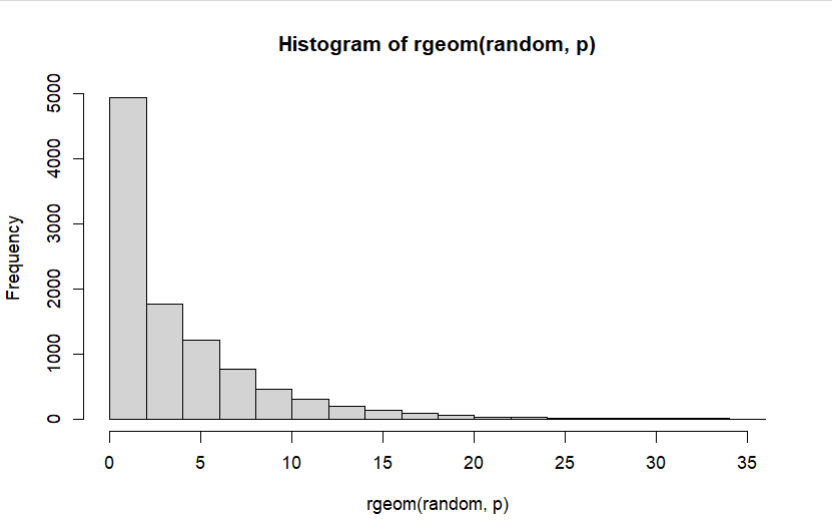
b) Mean Distribusi Geometrik dengan 10000 data random dapat diperoleh dengan menggunakan fungsi rgeom(random, p), di mana random = 10000 dan p = 0.2
Diperoleh hasil yang berbeda-beda namun mendekati 0.1024
c) Perbandingan hasil pada poin a dan b
Pada poin a diperoleh nilai tetap sebesar 0.1024, sementara pada poin b diperoleh hasil yang berbeda-beda namun selalu mendekati 0.1024. Hal ini menunjukkan bahwa rataan dari Distribusi Geometrik data random memiliki nilai yang selalu mendekati peluang Distribusi Geometrik.
d) Histogram Distribusi Geometrik dapat dibuat dengan menggunakan fungsi hist(rgeom(random, p)), di mana random = 10000 dan p = 0.2
e) Rataan (μ) dan Varian (σ²) Distribusi Geometrik dapat diperoleh dengan menggunakan persamaan μ = 1/p dan σ² = (1-p)/p², di mana p = 0.2
Diperoleh rataan sebesar 5 dan varian sebesar 20
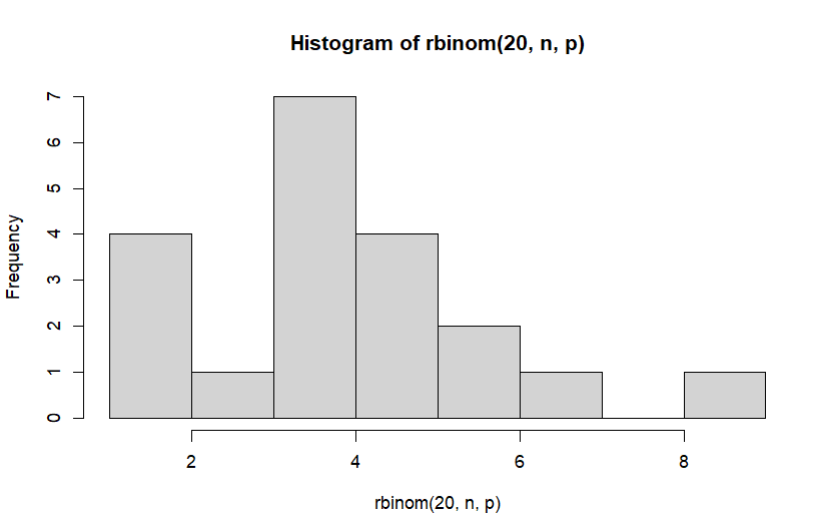
a) Peluang Distribusi Binomial dapat diperoleh dengan menggunakan fungsi dbinom(x, n, p), di mana x = 4, n = 20, dan p = 0.2
Diperoleh hasil sebesar 0.218199401946101
b) Histogram Distribusi Binomial dengan 20 data random dapat dibuat dengan menggunakan fungsi hist(rbinom(20, n, p)), di mana n = 20 dan p = 0.2
c) Rataan (μ) dan Varian (σ²) Distribusi Binomial dapat diperoleh dengan menggunakan persamaan μ = n * p dan σ² = n * p * (1-p), di mana n = 20 dan p = 0.2
Diperoleh rataan sebesar 4 dan varian sebesar 3.2
a) Peluang Distribusi Poisson dapat diperoleh dengan menggunakan fungsi dpois(x, lambda), di mana x = 6 dan lambda = 4.5
Diperoleh hasil sebesar 0.128120143864584
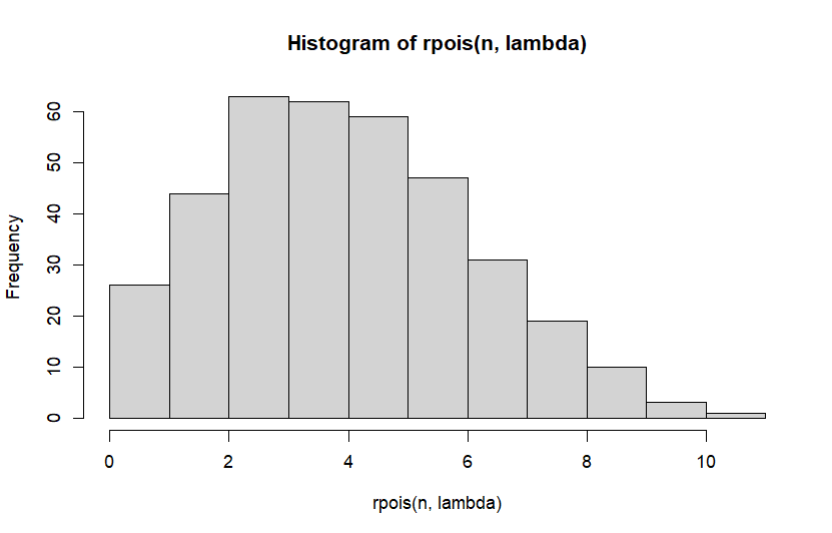
b) Histogram Distribusi Poisson dapat dibuat dengan menggunakan fungsi hist(rpois(n,lambda)), di mana n = 365 dan lambda = 4.5
c) Perbandingan hasil pada poin a dan b
Pada poin a diketahui besarnya rata-rata historis bayi lahir sebesar 4.5, sementara pada poin b diperoleh rataan dari 365 data random memiliki nilai yang mendekati 4.5. Hal ini menunjukkan bahwa rataan dari Distribusi Poisson data random memiliki nilai yang selalu mendekati Peluang Distribusi Poisson
d) Rataan (μ) dan Varian (σ²) Distribusi Poisson dapat diperoleh dengan menggunakan persamaan μ = lambda dan σ² = lambda, di mana lambda = 4.5
Diperoleh rataan dan varian sebesar 4.5
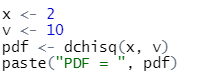
a) Fungsi probabilitas Distribusi Chi-Square dapat diperoleh dengan menggunakan fungsi dchisq(x, v), di mana x = 2 dan v = 10
Diperoleh hasil sebesar 0.00766415502440505
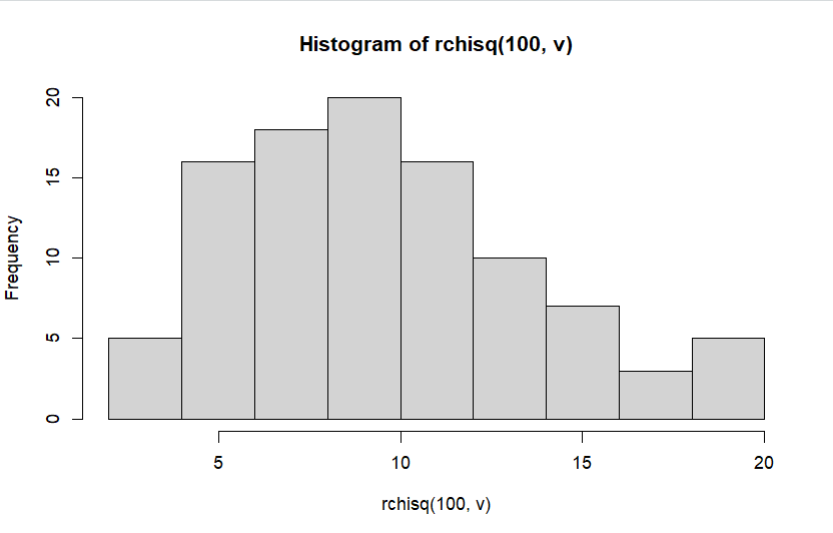
b) Histogram Distribusi Chi-Square dengan 100 data random dapat dibuat dengan menggunakan fungsi hist(rchisq(100, v)), di mana v = 10
c) Rataan (μ) dan Varian (σ²) Distribusi Chi-Square dapat diperoleh dengan menggunakan persamaan μ = v dan σ² = 2 * v, di mana v = 10
Diperoleh rataan sebesar 10 dan varian sebesar 20
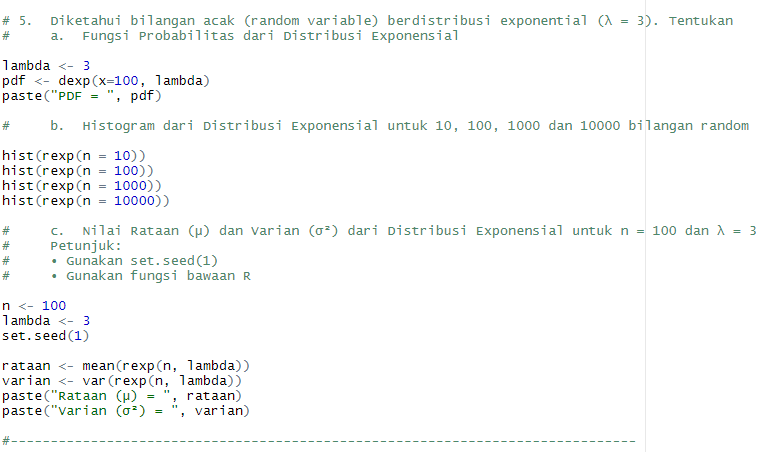
a) Fungsi probabilitas Distribusi Exponensial dapat diperoleh dengan menggunakan fungsi dexp(x=100, lambda), di mana lambda = 3
Diperoleh hasil sebesar 1.5444600667236e-130
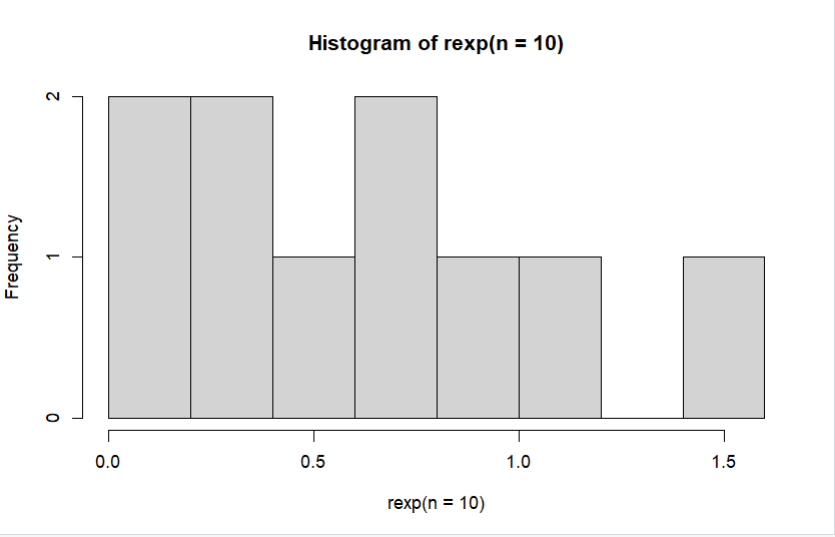
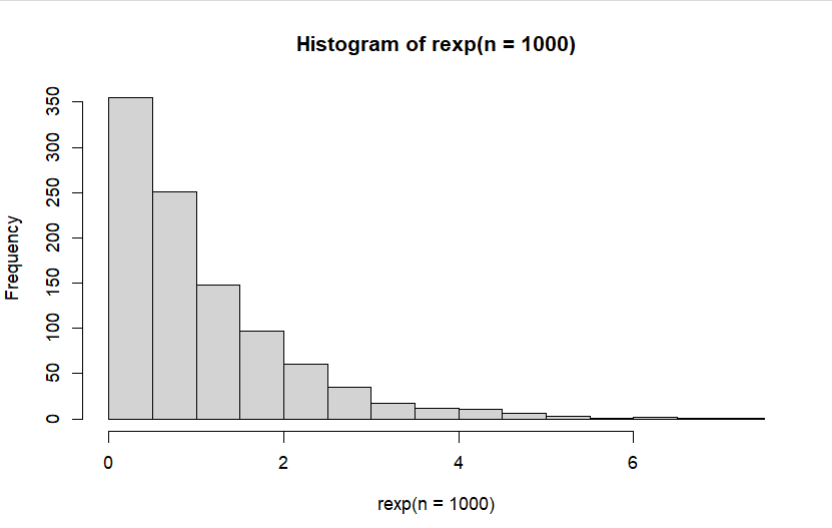
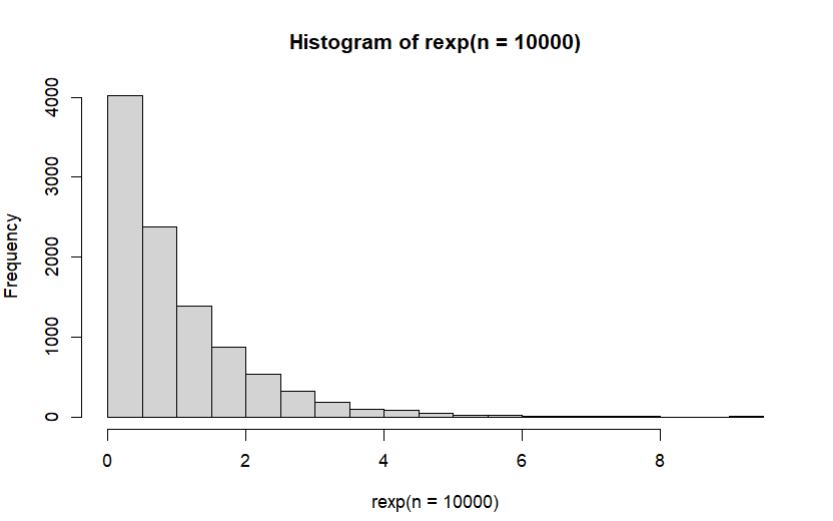
b) Histogram Distribusi Exponensial untuk 10, 100, 1000, dan 10000 bilangan random dapat dibuat dengan menggunakan fungsi hist(rexp(n)), di mana n = 10, 100, 1000, dan 10000
c) Rataan (μ) dan Varian (σ²) Distribusi Exponensial dapat diperoleh dengan menggunakan fungsi mean(rexp(n, lambda)) dan var(rexp(n, lambda)), di mana n = 100 dan lambda = 3
Diperoleh rataan sebesar 0.343558812019206 dan varian sebesar 0.0656076521452312
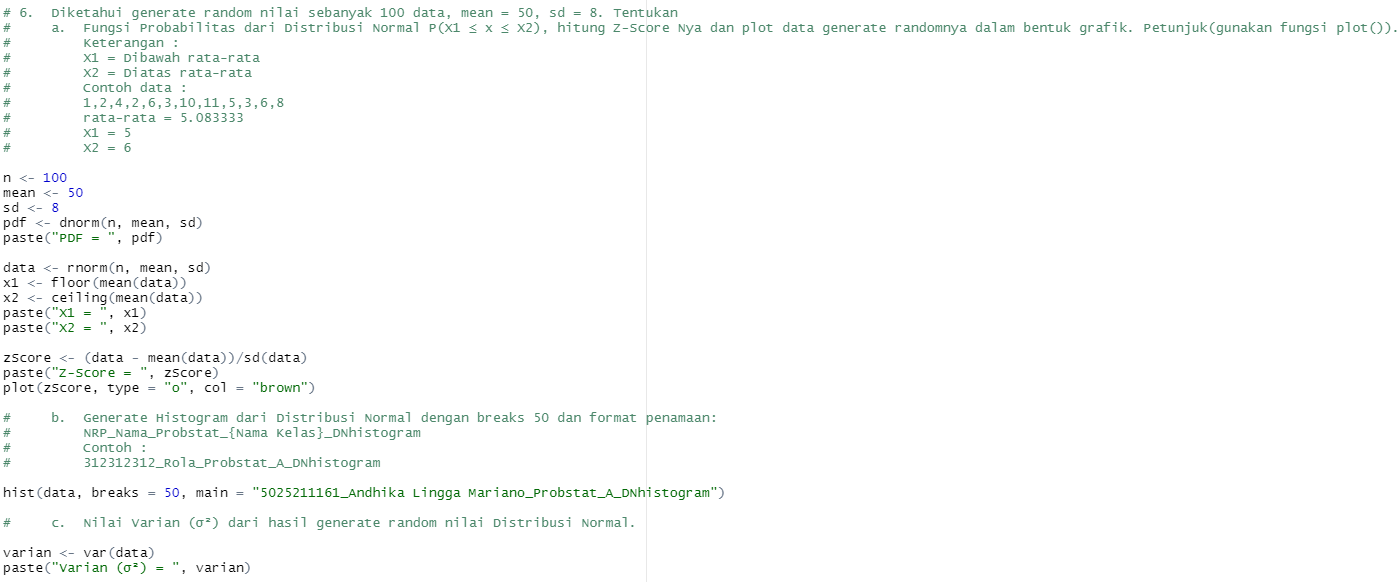
a) Fungsi probabilitas Distribusi Normal dapat diperoleh dengan menggunakan fungsi dnorm(n, mean, sd), di mana n = 100, mean = 50, dan sd = 8
Diperoleh hasil sebesar 1.64250227269486e-10
x1 dan x2 dapat diperoleh menggunakan fungsi floor(mean(data)) dan ceiling(mean(data)), di mana data = rnorm(n, mean, sd)
Diperoleh x1 sebesar 49 dan x2 sebesar 50
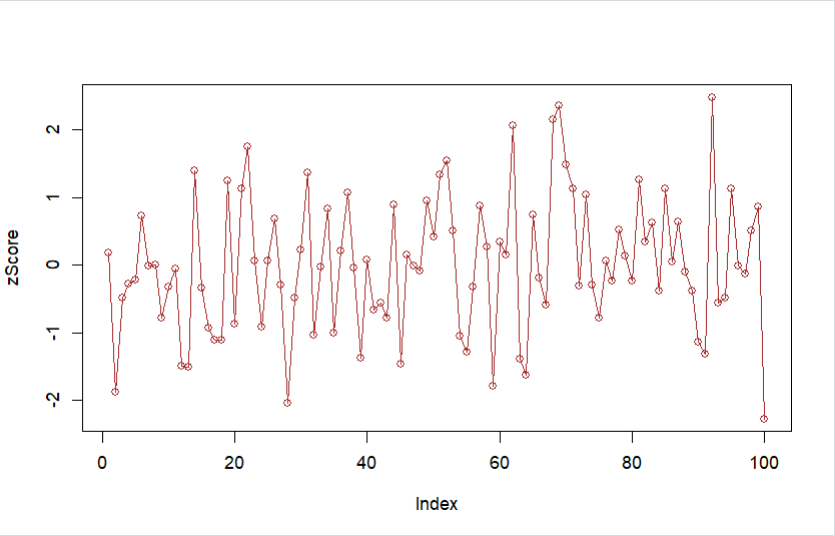
Z-Score pada Distribusi Normal dapat diperoleh dengan menggunakan persamaan zScore = (data - mean(data))/sd(data), di mana data = rnorm(n, mean, sd)
Plot data generate random dapat dibuat dengan menggunakan fungsi plot(zScore, type = "o", col = "brown")
b) Histogram Distribusi Normal dengan breaks 50 dan format penamaan NRP_Nama_Probstat_{Nama Kelas}_DNhistogram dapat dibuat dengan menggunakan fungsi hist(data, breaks = 50, main = "5025211161_Andhika Lingga Mariano_Probstat_A_DNhistogram"), di mana data = rnorm(n, mean, sd)
c) Varian (σ²) dari hasil generate random Distribusi Normal dapat diperoleh dengan menggunakan fungsi var(data), di mana data = rnorm(n, mean, sd)
Diperoleh varian sebesar 69.3173553177102