Weird Side Effects of `loadparams!`

[FelixBenning]

I am posting a picture of the pluto notebook for better understanding/readability (what are the outputs etc). Below you can find copyable code.

Copyable Code

begin
	using Flux:Flux
	using MLDatasets: MNIST
	using LinearAlgebra: norm, LinearAlgebra
end

MNIST.download(i_accept_the_terms_of_use=true)

begin
	x_train, y_train = MNIST.traindata()
	x_train = Float32.(x_train)
	y_train_oh = Flux.onehotbatch(y_train, 0:9)
	size(x_train), size(y_train), size(y_train_oh)
end

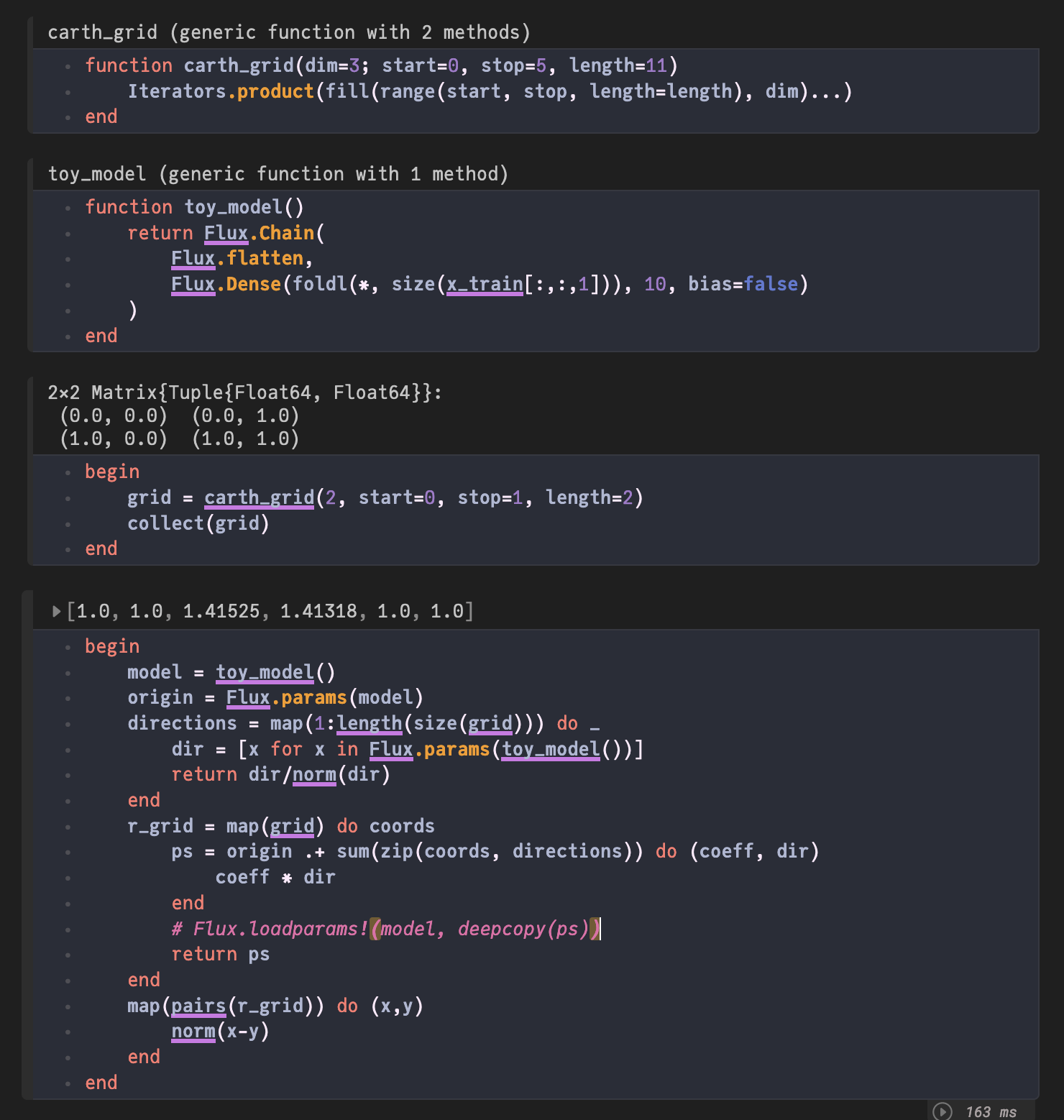
function carth_grid(dim=3; start=0, stop=5, length=11)
	Iterators.product(fill(range(start, stop, length=length), dim)...)
end


function toy_model()
	return Flux.Chain(
		Flux.flatten,
		Flux.Dense(foldl(*, size(x_train[:,:,1])), 10, bias=false)
	)
end

begin
	grid = carth_grid(2, start=0, stop=1, length=2)
	collect(grid)
end

begin
	model = toy_model()
	origin = Flux.params(model)
	directions = map(1:length(size(grid))) do _
		dir = [x for x in Flux.params(toy_model())]
		return dir/norm(dir)
	end
	r_grid = map(grid) do coords
		ps = origin .+ sum(zip(coords, directions)) do (coeff, dir)
			coeff * dir
		end
		# Flux.loadparams!(model, deepcopy(ps))
		return ps
	end
	map(pairs(r_grid)) do (x,y)
		norm(x-y)
	end
end

Okay so what is happening? I define a generator of a model toy_model, to essentially generate different parameter initializations. Because apparently that is faster than using loadparams #1764 and I can use the default initializer to get a more realistic distribution over initializations. Then I sample two prameter vectors from this distribution and normalize them. Since they are random with high dimension, they are very likely to be almost orthogonal. So due to normalization we get orthonormal vectors. So when I create the grid using the coordinates from a carthesian grid, I am essentially doing an orthonormal basis change.

Okay, so far so good. Now when I determine the distances of all the points on the new grid, the end result should be the same as before the basis change. Now the longest distance is between the points (0,0) and (1,1). Which is the squareroot of 2. So ~1.4. And that is in fact the largets value of the output. Nice! Everything works as intended.

But if I comment in the Flux.loadparams! my new output makes no sense

[1.0, 1.41621, 2.83242, 1.0, 2.23859, 1.41621]

This implies that loadparams! somehow modifies ps even through the deepcopy?

[FelixBenning]

I guess this is a good example, why parameters of a model should not be implicit. Normalizing them etc. was also a pain in the ass, as you can not use norm on the Flux.Params object directly, so I had to do the [x for x in Flux.params(...)] thing. This entire thing would be so much easier if you wouldn't have to keep track of some form of hidden state. But tensorflow/pytorch aren't any better, and I want to use some built in elements.

[darsnack]

Not at the computer, but a quick suggestion would be to use Flux.fmap (from Functors.jl) to modify the parameters instead of dealing with Params. Similarly use loadmodel! instead of loadparams! (the latter is something we eventually want to deprecate). Both of these functions are the explicit alternatives to working with Params.

[FelixBenning]

Both fmap and loadmodel force a one to one relation between models and params. But I want to generate a grid of params and then try them out, plugging them into the model. So after I generated two directions of parameter vectors (by creating the model multiple times, which is already somewhat confusing), I use those directions to define a grid of parameters. Let us for example consider the point (1,2) This implies I want to add one times the first parameter direction, to two times the second parameter direction. Okay I can fmap the second parameter vector with x->2*x. But I still need to add them together. Now if they are both part of their models and I can't work with the parameters directly, that is impossible. fmap does not really allow me to zip two or more models (depending on the dimension of my grid). loadmodel is not helpful since I don't want to just dump/restore models to json/bson. I want to do arithmetic on the parameter vectors.

[ToucheSir]

First things first: deepcopy is poorly named and really just does a bitwise memcpy of the object. In this case, it leaves the actual interesting bits of Params (namely the internal reference to a list of arrays) fully intact. Something like Params(map(copy, ps)) will avoid any unwanted mutation.

Both fmap and loadmodel force a one to one relation between models and params...
fmap does not really allow me to zip two or more models (depending on the dimension of my grid).

You're in luck, because it does :)

model1, model2 = ...

i = Ref(1) # avoids boxing
newmodel = fmap(model1, model2) do p1, p2
  c1, c2 = grid[i[]]
  i[] += 1
  return @. c1 * p1 + c2 * p2
end

[darsnack]

Looks like Brian beat me to the punch, but I already typed this out, so here it is.

---

Okay let me see if I understand the problem statement correctly. You have a "model distribution" induced by the initialization functions. You want to take two samples from this distribution (or do you want to sample two parameters from a single initialization? I was confused on this point). Then we think of these two model initializations as a flat vector of parameters in parameter space. We normalize them to make them unit vectors. They are also extremely likely to be orthogonal, giving me an orthonormal basis. Then I define a Cartesian grid of coordinates, allowing me to explore linear combinations of my basis.

If the above is correct, then you could try the following.

Explicit option

This one is admittedly more complex, mostly because we haven't exposed using Functors.jl except in the most basic cases. There's work to be done to make this more friendly for users.

using Flux
using Flux: fmap, destructure, trainable, functor

# this would eventually be something a user does not define
function walk_trainable(f, x, ys...)
    func, re = functor(x)
    ts = trainable(func)
    yfuncs = map(y -> functor(typeof(x), y)[1], ys)
    result = map(func, yfuncs...) do zs...
         (zs[1] in ts) ? f(zs...) : zs[1]
    end
    
    return re(result)
end

function normalize_model(m)
    flat, rebuild = destructure(m)
    
    return rebuild(flat / norm(flat))
end

function combine_models(coefficients, models)
    scaled_models = map(coefficients, models) do scale, m
        fmap(m; walk = walk_trainable) do p
            scale .* p
        end
    end
    combined_model = fmap(sum, scaled_models...; walk = walk_trainable)
    
    return combined_model
end

model_samples = [normalize_model(toy_model()) for _ in grid_cardinality]
grid = # make the grid

results = map(grid) do coefficients
    combine_models(coefficients, models)
end

Another option using destructure for everything.

using Flux
using Flux: destructure

function normalize_model(m)
    flat, rebuild = destructure(m)
    
    return rebuild(flat / norm(flat))
end

function combine_models(coefficients, models)
    flat, rebuild = destructure(models[1])
    flats = [destructure(m)[1] for m in models[2:end]]
    pushfirst!(flats, flat)
    combined_flats = mapreduce(coefficients, +, flats) do c, p
        c .* p
    end
    
    return rebuild(combined_flats)
end

model_samples = [normalize_model(toy_model()) for _ in grid_cardinality]
grid = # make the grid

results = map(grid) do coefficients
    combine_models(coefficients, models)
end

Implicit option

using Flux
using Flux: Params, params

# even here it might be better to use destructure
# but I am sticking with implicit on purpose
function normalize_params!(model)
    ps = params(model)
    flat = mapreduce(vec, vcat, ps)
    flat .= flat ./ norm(flat)
    copy!(ps, flat)
    
    return model
end

function combine_models!(dst, coefficients, models)
    ps = params(dst)
    ps .= coefficients[1] .* params(models[1])
    for (c, m) in zip(coefficients, models[2:end])
        ps .= ps .+ c .* params(m)
    end
    
    return dst
end

model_samples = [normalize_params!(toy_model()) for _ in grid_cardinality]
grid = # make the grid

dst = toy_model()
results = map(grid) do coefficients
    combine_models!(dst, coefficients, models)
end

[FelixBenning]

Thank you for all the suggestions - I'll give it another shot tomorrow :)

[FelixBenning]

Okay I had some time to properly read your comments:

1. @ToucheSir

First things first: deepcopy is poorly named and really just does a bitwise memcpy of the object. In this case, it leaves the actual interesting bits of Params (namely the internal reference to a list of arrays) fully intact. Something like Params(map(copy, ps)) will avoid any unwanted mutation.

That sounds like a bug. I mean that sounds very much like a shallow copy not a deepcopy.

https://github.com/JuliaLang/julia/blob/master/base/deepcopy.jl

deepcopy(x)
Create a deep copy of x: everything is copied recursively, resulting in a fully
independent object. For example, deep-copying an array produces a new array whose elements
are deep copies of the original elements. Calling deepcopy on an object should generally
have the same effect as serializing and then deserializing it.

I still would expect loadparams! to only modify the first parameter and not the second, but if that is on its way out I guess there is no point beating a dead horse.

2. @darsnack

Your first interpretation is correct I think. I did not completely understand the walk_trainable function yet.

I guess the main takeaway from this is that you do inted to identify parameters and models. And I am starting to understand that philosophy, reading about Functors. What I am a bit confused about is this description of functor in
Functors.jl:

functor returns the parts of the object that can be inspected, as well as a re function that takes those values and restructures them back into an object of the original type.

That sounds on the surface identical to the (currently undocumented) destructure function, which seems to return a destructured parameter object that can be inspected and a rebuild function. If I understood this correctly, then they are the same thing. If that is the case and you decide to cut away one name, it might be relevant, that I did not really understand functor until I realized it does the same as destructure. So I think the name destructure is much more helpful conveying what it does than functor.

EDIT: it also makes much more sense to "destructure a Functor" than to "functor a Functor"

[darsnack]

I did not completely understand the walk_trainable function yet.

You can think of a functor as a tree of nodes representing the model, with the array parameters as the leaves (as well as things like activations, convolution kernel parameters, etc.). fmap will walk this tree using the walk function. walk is responsible for calling functor to take apart one level of the tree and recurse into each child node. The first argument to walk is a function f that should be called on the children to recurse them. The rest of the arguments are the current nodes in the tree(s). In our case, we only want to recurse into the child nodes marked trainable in Flux. This is why we have walk_trainable instead of using the default walk function.

That sounds on the surface identical to the (currently undocumented) destructure function, which seems to return a destructured parameter object that can be inspected and a rebuild function.

Yes they are very similar. destructure is built on top of functor. functor returns the parameters but as a tree structure made of nested named tuples. destructure goes one step further and flattens this nested structure into a vector (while tracking some extra information so that the flat vector can be mapped back to the nested structure).

In terms of naming, we have #1946 for exactly this reason, because we agree that functor is a poor and confusing name.

[FelixBenning]

Something which made me uncomfortable using this destructure technique: We are assuming that the restructure method is the same if I destructure two models generated by the same model factory. This is extremely likely to be true for any reasonable implementation of the destructure method, but it makes assumptions about the implementation of destructure. I.e. I can throw away the restructure method for all but the first destructuring. I am also not sure how to improve on this though...

I mean if the model was a class, this could be a class method. But they are in general anonymous structs generated by Chaining other model structs together. Throwing away a result all the time also feels wasteful performance wise.

[darsnack]

Most of the cost is walking the model which you have to do no matter what. The rebuild method of each model is cheap to throw away, I think. It only stores a vector of offsets and the total parameter length (see here). You do pay some cost, of course, but it should be nearly negligible compared to evaluating the model or taking gradients.

But the larger problem of assuming the models are the same structure...if they weren't, then the concept of linear combinations of them wouldn't make sense. You could add checks to walk_trainable to make sure the child nodes are the same. loadmodel! is one example where we do this, because you want to be very particular and conservative about loading one model into another. These kinds of checks should be built into fmap or whatever the user facing function is. Doing the checks with destructure is trickier cause you only walk a single model at a time.

[ToucheSir]

First things first: deepcopy is poorly named and really just does a bitwise memcpy of the object. In this case, it leaves the actual interesting bits of Params (namely the internal reference to a list of arrays) fully intact. Something like Params(map(copy, ps)) will avoid any unwanted mutation.

That sounds like a bug. I mean that sounds very much like a shallow copy not a deepcopy.

I agree, it's really designed for bitstypes where a bitwise copy is a deep copy. There are many threads out there where core devs have explicitly disavowed people from using it, but I'm not sure if forbidding its use at the language level is possible without making breaking changes. For our part we could override deepcopy to error, but then that raises the question of where we stop: do we override deepcopy for every struct in Flux which might contain mutable arrays?

On destructure: in an ideal world, Flux would not expose this function. We (by which I mean mostly @mcabbott) spent an extraordinary amount of time trying to refactor it to be "safer" for Flux 0.13/Optimisers.jl (which is also where the docs are). Now that Lux.jl is out and natively supports taking a ComponentArray as input, I've a mind to put it on the chopping block for 0.14.

But that's not really important here since you need not touch destructure at all for your use case. For example, you could use fmapstructure to convert each model you sample into a nested (named)tuple tree. Combine that with Flatten.jl or a similar package, and you can literally zip parameters + grid coefficients. To resuscitate the tree into a model, one or both of 2-arg fmap or loadmodel! should work.

[FelixBenning]

@ToucheSir I like the destructure/restructure mechanic actually. It is quite readable and side effect free judging by the lack of !. Using loadmodel! doesn't have that property, and also with fmap there would be at least another copy if I understand what you are suggesting (flatten the model, do the transformation, load back into model with fmap). I mean then you are using fmap like a restructure function. Just with less readability.

[ToucheSir]

It's exactly the opposite: destructure/restructure may induce a copy for some parameters (the former definitely will), whereas handling the nested structure using fmap and co. are guaranteed not to add any extra ones (modulo what you yourself allocate in the callback).